Расстановка, или Схемы хеширования

Руслан Богатырев, Андрей Шилов
15.06.2001
Мир ПК, #06/2001

В мире алгоритмов

С хешированием мы сталкиваемся едва ли не на каждом шагу: при работе с браузером (список Web-ссылок), текстовым редактором и переводчиком (словарь), языками скриптов (Perl, Python, PHP и др.), компилятором (таблица символов). По словам Брайана Кернигана, это «одно из величайших изобретений информатики». Заглядывая в адресную книгу, энциклопедию, алфавитный указатель, мы даже не задумываемся, что упорядочение по алфавиту является не чем иным, как хешированием.

Хеширование есть разбиение множества ключей (однозначно характеризующих элементы хранения и представленных, как правило, в виде текстовых строк или чисел) на непересекающиеся подмножества (наборы элементов), обладающие определенным свойством. Это свойство описывается функцией хеширования, или хеш-функцией, и называется хеш-адресом. Решение обратной задачи возложено на хеш-структуры (хеш-таблицы): по хеш-адресу они обеспечивают быстрый доступ к нужному элементу. В идеале для задач поиска хеш-адрес должен быть уникальным, чтобы за одно обращение получить доступ к элементу, характеризуемому заданным ключом (совершенная хеш-функция). Однако на практике идеал приходится заменять компромиссом и исходить из того, что получающиеся наборы с одинаковым хеш-адресом содержат более одного элемента.

Термин «хеширование» (hashing) в печатных работах по программированию появился сравнительно недавно (1967 г. [1]), хотя сам механизм был известен и ранее. Глагол «hash» в английском языке означает «рубить, крошить», т. е. создавать этакий «винегрет». Для русского языка академиком А.П. Ершовым [2] был предложен достаточно удачный эквивалент – «расстановка», созвучный с родственными понятиями комбинаторики, такими как «подстановка» и «перестановка». Однако пока он не прижился.

Как отмечает Дональд Кнут [3], идея хеширования впервые была высказана Г.П. Ланом при создании внутреннего меморандума IBM в январе 1953 г. с предложением использовать для разрешения коллизий хеш-адресов метод цепочек. В открытой печати хеширование впервые было описано Арнольдом Думи (1956), указавшим, что в качестве хеш-адреса удобно использовать остаток от деления на простое число. Подход к хешированию, отличный от метода цепочек, был предложен А.П. Ершовым (1957), который разработал и описал метод линейной открытой адресации. Среди других исследований можно отметить работы Петерсона (1957, [4]) и Морриса (1968, [5]). В первой реализовывался класс методов с открытой адресацией при работе с большими файлами, а во второй давался обширный обзор по хешированию и вводился термин «рассеянная память» (scatter storage).

Массивы – предшественники хеш-структур

Одна из важных задач, решаемых в программировании,– это обеспечение быстрого (прямого) доступа к данным по некоему коду (индексу, адресу). Неудивительно, что решающий эту задачу массив стал одним из главных строительных блоков, превосходя по использованию списки, которые определяют последовательный доступ к элементам. В математике массиву соответствуют понятия вектор (в одномерном случае) и матрица (в двумерном).

Как известно, массив задает отображение (A) множества индексов (I) на множество элементов (E), т. е. A: I —> E. Массив позволяет по индексу быстро найти требуемый элемент. Хеширование решает в точности такую же задачу. Однако здесь уже в роли индекса выступает хеш-адрес, который определяется как значение некоей хеш-функции, применяемой к уникальному ключу. В этом смысле хеш-структуры можно рассматривать как обобщение массива.

В программировании зависимость между индексом и значением записывается в виде: A = ARRAY I OF E. В роли индексирующего типа (I) обычно выбирается конкретный диапазон значений из целочисленного типа (хотя в общем случае в их роли могут выступать так называемые скалярные типы, т. е. булев тип, перечисления, множества и др.). Ну а элементы массива в зависимости от языка программирования могут быть любыми, начиная от битов, чисел и указателей (ссылок) и заканчивая составными типами произвольной глубины.

То, что массив задает функцию отображения, в языке Ада подчеркивается даже на уровне синтаксиса. Например, при появлении в тексте программы записи вида «a(i)» трудно с ходу сказать, идет ли это обращение к i-му элементу массива «a» или же просто вызывается функция «a» с параметром «i».

Выделяют два разных вида массивов: одномерные (наиболее общий случай) и многомерные (на каждом слое адресации используется массив фиксированной структуры). Во втором случае есть и особый подвид: ступенчатые массивы (jagged arrays). Они встречаются, в частности, в языке C# в том случае, когда на каждом слое адресации используется массив переменной структуры. Иначе говоря, здесь мы имеем дело с массивом разных массивов. В других языках такая конструкция легко описывается массивом разнородных указателей (каждый указывает на массив своей структуры), что фактически определяет массив списков.

Интересно, что Н. Вирт после многих лет использования в своих языках (Паскаль, Модула-2) в качестве индексирующего типа разных скалярных типов пришел к выводу, что лаконичное решение, воплощенное в языке Си (а точнее, унаследованное в Си от языков BCPL и B), носит куда более практичный характер. И в своих новых языках Оберон и Оберон-2 он отказался от идей Паскаля и ограничился заданием размера массива (количества индексируемых элементов), т. е. определением для индексов диапазона 0...n—1, где n – это размер массива: A = ARRAY 16 OF E. Связано это с эффективностью реализации и с активным использованием в программировании элементов модулярной арифметики. В Обероне предопределенная функция MOD («x MOD n»), как и в математике, соответствует остатку от целочисленного деления «x» на «n». Как показывает опыт, использование 0 в качестве начального индекса удобно в подавляющем большинстве задач. Механизмы хеширования опираются точно на ту же основу.

Математика и программирование

Вспомним некоторые определения из курса элементарной математики. Отображением (f: A —> B) множества A во множество B (функцией на A со значениями в B) называется правило, по которому каждому элементу множества A сопоставляется один или несколько элементов множества B. Отсюда следует, что отображения могут быть однозначными и многозначными в зависимости от того, имеет ли каждый прообраз в соответствии один или несколько образов. Однозначное отображение f: A—> B называется сюръективным (сюръекцией), если f(A) = B. Это так называемое отображение «на». Отображение (в общем случае неоднозначное) называется инъективным, если образы различных прообразов различны (отображение «в»). Cюръективное и инъективное отображение называется биекцией.

Вот теперь, пользуясь этими понятиями, попробуем разобраться в природе хеширования. Итак, одномерные и многомерные массивы – это яркий пример сюръекции. Поэтому их можно назвать «сюръективными» массивами. Биекцию в общем случае они не задают, поскольку разным индексам (прообразам) могут соответствовать одни и те же значения (образы). Примером «биективного» массива может служить, например, соответствующим образом заполненный массив литер: ARRAY 256 OF CHAR.

В реальных задачах нередко возникают ситуации, когда не столько важно иметь однозначное соответствие между адресом и значением, сколько гарантию того, что одно и то же значение не может быть получено по разным адресам. А это и есть инъекция, реализуемая через хеширование. Следовательно, в случае хеширования значения хранятся в «инъективных» массивах разной структуры. Именно здесь проходит водораздел между разными схемами и методами хеширования. Именно отсюда и проистекают проблемы поиска оптимального баланса между пространством хранения и временем доступа.

Схемы хеширования

Традиционно принято выделять две схемы хеширования:

хеширование с цепочками (со списками);
хеширование с открытой адресацией.

В первом случае выбирается некая хеш-функция h(k) = i, где i трактуется как индекс в таблице списков t. Поскольку нельзя гарантировать, что не встретится двух разных ключей, которым соответствует один и тот же индекс i (конфликт, коллизия), такие «однородные» ключи просто помещаются в список, начинающийся в i-ячейке хеш-таблицы t (см. рисунок). Очевидно, что процесс заполнения хеш-таблицы будет достаточно простым, но при этом доступ к элементам потребует двух операций: вычисления индекса и поиска в соответствующем списке. Операции по занесению и поиску элементов при таком виде хеширования будут вестись в незамкнутом (открытом) пространстве памяти.

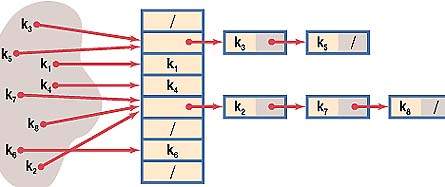Отображение ключей путем хеширования с цепочками

Во втором случае все операции производятся в одном измерении, и таблица t является обычным одномерным массивом. Однако в этом случае подход к разрешению коллизий индексов иной: либо элементы с «однородными» ключами пытаются размещать в непосредственной близости от полученного индекса, либо осуществляют многократное хеширование (обычно двойное), когда для хорошего перемешивания последовательно применяется набор разных (взаимосвязанных) хеш-функций. Очевидно, что здесь и заполнение хеш-таблицы, и доступ к элементам будет весьма замысловатым. Хеш-адрес элемента с данным ключом как бы открыт: он постепенно уточняется. При этом все операции ведутся в замкнутом пространстве (в одномерном массиве).

Как нетрудно заметить, традиционная классификация методов хеширования может быть заменена другими: хеширование с цепочками можно относить по классификации Ахо, Хопкрофта и Ульмана [6] к так называемому «открытому» хешированию (в данной статье – к многомерному хешированию, поскольку при использовании списков речь идет о нескольких измерениях), а хеширование с открытой адресацией – к «закрытому» хешированию (одномерному).

Реализация хеш-таблиц

На практике нередко задача упрощается тем, что вместо пары «ключ—элемент» в хеш-таблицу достаточно заносить только ключи, поскольку ключ нередко совпадает с самим элементом (в случае текстовых строк и чисел). Если это не так, то необходимо хранить рядом и ссылки на соответствующие элементы.

Прежде чем рассматривать схемы и соответствующие им методы хеширования, давайте остановимся на спецификации модуля, в котором реализуются обсуждаемые ниже методы.

Листинг 1. Интерфейс модуля HashTable

DEFINITION HashTable;

  PROCEDURE Ins (t: T; k: Key;
 i: Item);
  PROCEDURE Get (t: T; k: Key;
 VAR i: Item):
 BOOLEAN;  
  PROCEDURE Del (t: T; k: Key;
 VAR i: Item):
 BOOLEAN;


  PROCEDURE Hash       (k: Key):
 INTEGER;
  PROCEDURE DoubleHash (k: Key):
 INTEGER;

  PROCEDURE Init  (VAR t: T; size:
 INTEGER;
 multi: BOOLEAN);
  PROCEDURE Size  (t: T):
 INTEGER; 
  PROCEDURE Clear (t: T);

END HashTable.

Взгляните на листинг 1. Здесь представлена интерфейсная часть модуля HashTable. В нем используются три абстрактных типа данных (или класса), обозначающих собственно хеш-таблицы (T), ключи (Key) и элементы (Item). Основными операциями, реализованными в виде процедур-функций, являются Ins (занесение элемента в таблицу) и Get (доступ к элементу по ключу). Вне зависимости от используемого метода хеширования процедура занесения элемента делится на три этапа:

вычисление хеш-адреса (по хеш-функции);
уточнение хеш-адреса (в случае коллизии);
размещение ключа (и/или элемента).

Выбор хеш-функции – непростая задача. Такая функция должна удовлетворять двум требованиям: предусматривать быстрое вычисление и минимизировать количество коллизий. Самый простой вид хеш-функции: h(k) = k MOD M, где k – ключ-число, M – размер хеш-таблицы (простое число), MOD – остаток от целочисленного деления. Если ключ k – составной (состоит из нескольких слов/символов x₁ ... x_s), можно воспользоваться идеей Дж. Картера и М. Вегмана (1977): h(k) = (h₁(x₁) + h₂(x₂) + ... + h_s(x_s)) MOD M. На практике для выбора хеш-функции применяются различные эвристические подходы, учитывающие специфику задач.

Вопросы вычисления и уточнения хеш-адреса с алгоритмической точки зрения являются ключевыми, и на них мы остановимся при разборе схем хеширования.

Листинг 2. Внутренние структуры данных

TYPE
    Map = POINTER TO MapRec;
    MapRec = RECORD
               key : Key;
               item: Item
             END;

    MultiMap = POINTER TO MultiMapRec;
    MultiMapRec = RECORD (MapRec)
                    next: MultiMap;
                  END;

    T = ARRAY OF Map;

Внутренние структуры данных, реализующие таблицу хеширования, представлены на листинге 2. Здесь класс Map и подкласс MultiMap (в терминологии языков Оберон и Оберон-2 «расширение типа» Map) отвечают за хранение пар «ключ-элемент». Сама же хеш-таблица t представлена в виде открытого массива c объектами класса Map.

При оценке эффективности алгоритмов нередко упускают из вида, что доступ к элементу (массива) хотя и быстрый, но отнюдь не мгновенный (как в математике). Он реализуется через набор инструкций, которые определяются соответствующим компилятором, средой исполнения (виртуальная машина, машинный код) и аппаратной платформой. При хешировании для реализации метода важно также знать, где хранятся ключи и элементы: во внутренней (оперативной) или во внешней памяти.

В последнем случае уже не так важно, как долго будет вычисляться хеш-функция: гораздо большего внимания требует минимизация обращения к страницам (блокам) внешней памяти и работа внутри них.

Одномерное хеширование

В одномерном хешировании (открытая адресация) можно выделить два основных метода:

линейное исследование – В.Петерсон (1957), А.П.Ершов (1957);
двойное хеширование – Гюи де Бальбин (1968), Г.Кнотт (1968), Белл, Каман (1970), Р.Брент (1973).

Идея метода линейного исследования состоит в том, чтобы в случае коллизии просматривать соседние ячейки таблицы размером M до тех пор, пока не будет найден искомый ключ k или же пустая позиция. Обычно просмотр ведется в виде последовательности проб: h(k), h(k)–1, h(k)–2, ..., 0, M–1, ... h(k)+1. Чтобы избежать эффекта скучивания, шаг просмотра можно выбирать не равным 1, а в виде числа, взаимно простого с M. Это приводит к идее квадратичного исследования. Здесь для i-й пробы h(k,i) = (h(k) + c₁xi + c₂xi²) MOD M.

В случае линейного исследования нужно быть крайне осторожным с реализацией функции удаления (Del): можно потерять другой ключ. По этой причине прибегают к приему логического удаления: ячейку в таблице помечают соответствующим признаком. Таким образом, ячейки становятся трех видов: пустые, занятые и удаленные. Стоит заметить, что среднее число проб при успешном поиске с помощью этого метода зависит не от порядка вставки ключей, а только от числа ключей с конкретным хеш-адресом. Алгоритм хорошо работает в начале заполнения таблицы, но затем все чаще встречаются длинные серии проб. И все же он достаточно прост и эффективен: при заполнении таблицы на 90% для поиска элемента в среднем требуется около 5,5 пробы.

Двойное хеширование на этапе уточнения хеш-адреса использует не просмотр, а вычисление значения другой хеш-функции, т. е. применяет h₁(k) и h₂(k). Значения h₁(k) должны опять-таки лежать в диапазоне 0...M–1, а вот функция h₂(k) должна порождать значения от 1 до M–1, причем взаимно простые с M (если M – простое число, то h₂(k) – любое в указанном диапазоне, а если M = 2^p , то h₂(k) – нечетное). Если число занятых ячеек обозначить N, то среднее количество проб в этом алгоритме будет составлять (M+1) / (M–N+1).

Многомерное хеширование

Схема многомерного хеширования (метод цепочек, Ф. Уильямс, 1959) довольно проста: в случае возникновения коллизий после вычисления хеш-функции ключи с одним хеш-адресом соединяются в цепочку. Здесь приходится решать такую проблему, как обеспечение равномерности заполнения хеш-таблицы. К тому же было бы неплохо, если бы она оказалась достаточно сбалансированной, чтобы содержать предельно короткие цепочки. Интересно, что если таблица будет заполнена наполовину, среднее число проб при неудачном поиске составит 1,18. Если таблица будет заполнена полностью, то для нахождения элемента потребуется в среднем 1,8 пробы. Метод цепочек экономичен с точки зрения проб, но неэффективно расходует память. Интересный обзор эффективности методов вместе с демонстрационным Java-аплетом приведен в курсе канадского университета McGill по алгоритмам и структурам данных (www.cs.mcgill.ca/~cs251/OldCourses/ 1997/topic12).

Во всех наших рассуждениях следует, однако, иметь в виду, что среднее время, основанное на теории вероятностей, может значительно отличаться от реального в каждом конкретном случае. Так что несмотря на стройные математические выкладки, жизнь вносит свои существенные коррективы. Современные процессоры работают при тактовой частоте порядка 1 ГГц, соответственно каждый такт занимает 1 нс. Время доступа к оперативной памяти составляет 7—10 нс. Отсюда следует, что на каждое обращение к памяти времени требуется в 7—10 раз больше, чем на обработку инструкции процессора. При наличии кэш-памяти проблема частично решается, однако в общем случае такой разрыв на порядок будет сохраняться. Для хеширования желательно, чтобы элементы хранились как можно более компактно и ближе друг к другу, а это возможно как раз при одномерном хешировании.

Области применения и другие методы

Одно из побочных применений хеширования состоит в том, что оно создает своего рода слепок, «отпечаток пальца» для сообщения, текстовой строки, области памяти и т. п. Такой «отпечаток пальца» может стремиться как к «уникальности», так и к «похожести» (яркий пример слепка – контрольная сумма CRC). В этом качестве одной из важнейших областей применения является криптография. Здесь требования к хеш-функциям имеют свои особенности. Помимо скорости вычисления хеш-функции требуется значительно осложнить восстановление сообщения (ключа) по хеш-адресу. Соответственно необходимо затруднить нахождение другого сообщения с тем же хеш-адресом. При построении хеш-функции однонаправленного характера обычно используют функцию сжатия (выдает значение длины n при входных данных больше длины m и работает с несколькими входными блоками). При хешировании учитывается длина сообщения, чтобы исключить проблему появления одинаковых хеш-адресов для сообщений разной длины. Наибольшую известность имеют следующие хеш-функции [7]: MD4, MD5, RIPEMD-128 (128 бит), RIPEMD-160, SHA (160 бит). В российском стандарте цифровой подписи используется разработанная отечественными криптографами хеш-функция (256 бит) стандарта ГОСТ Р 34.11—94.

Хеширование можно рассматривать и как расстановку, и как снятие отпечатков, и как раскрашивание. В самом деле, то, что каждому ключу ставится в соответствие целое число, дает основание говорить о хеш-адресе как о хеш-краске.

Многомерное хеширование отражает известный принцип Дирихле: при любом размещении (n+1) предметов по «n» ящикам всегда найдется ящик с двумя предметами. В случае, если нас интересует наличие k предметов в одном ящике, он формулируется так: при любом размещении (rxk – r + 1) предметов по r ящикам найдется k предметов в одном ящике. Несмотря на свою тривиальность, принцип Дирихле весьма полезен – на нем основаны многие теоремы математики фундаментального характера (теоремы Матиясевича, Дирихле, Эйлера – Ферма, Рамсея). Если большая структура разбивается на непересекающиеся части, то наличие какой подструктуры можно гарантировать в одной из частей? И обратная задача: сколь богатой должна быть большая структура, чтобы любое ее разбиение содержало часть предписанной природы? Здесь разбиение множества ключей на цепочки («ящики») приводит к смежным задачам, в частности, к теории Рамсея – специальной ветви комбинаторики, которая имеет дело со структурами, сохраняющимися под действием разбиений.

Разумеется, методы и сферы применения хеширования не ограничиваются тем, что представлено в этой статье. Не вдаваясь в строгий анализ эффективности, мы рассматривали только базовые, наиболее известные методы. Помимо них можно отметить полиномиальное хеширование (М. Ханан и др., 1963), упорядоченное хеширование (О. Амбль, 1973), мультипликативное хеширование (Р. Флойд), хеширование Фибоначчи (Я. Одерфельд), расширяемое хеширование (Ю. Нивергельт и др., 1979), линейное хеширование (В. Литвин, 1980). Подробнее о методах хеширования см. [3, 6, 8—11].

Литература

1. Hellerman H. Digital Computer System Principles. McGraw-Hill, 1967.
2. Ершов А.П. Избранные труды. Новосибирск: ВО «Наука», 1994.
3. Кнут Д. Искусство программирования, т.3. М.: Вильямс, 2000.
4. Peterson W.W. Addressing for Random-Access Storage // IBM Journal of Research and Development. 1957. V.1, N2. Р.130—146.
5. Morris R. Scatter Storage Techniques // Communications of the ACM, 1968. V.11, N1. Р.38—44.
6. Ахо А., Хопкрофт Дж., Ульман Дж. Структуры данных и алгоритмы. М.: Вильямс, 2000.
7. Чмора А. Современная прикладная криптография. М.: Гелиос АРВ, 2001.
8. Кормен Т., Лейзерсон Ч., Ривест Р. Алгоритмы: построение и анализ. М.: МЦНМО, 2001.
9. Вирт Н. Алгоритмы + структуры данных = программы. М.: Мир, 1985.
10. Керниган Б., Пайк Р. Практика программирования. СПб.: Невский диалект, 2001.
11. Шень А. Программирование: теоремы и задачи. М.: МЦНМО, 1995.